
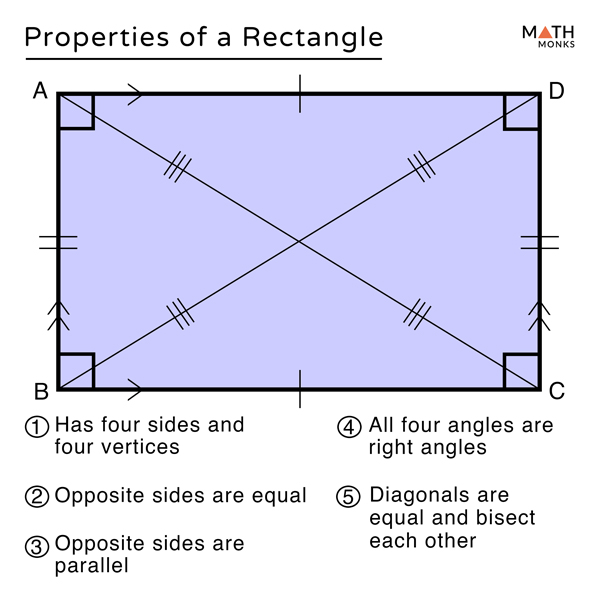
It is true that ‘If a number is a multiple of 4, then it is even’, but it is false that ‘If a number is even, then it is a multiple of 4’. Remember that a statement may be true, but its converse false. If two angles of a triangle are equal, then the sides opposite those angles are equal.Now the corresponding test for a triangle to be isosceles is clearly the converse statement: If two sides of a triangle are equal, then the angles opposite those sides are equal.This property can be re-formulated as an ‘If …, then … ’ statement: For example, the fact that the base angles of an isosceles triangle are equal is a property of isosceles triangles. Most of the tests that we meet are converses of properties that have already been proven.
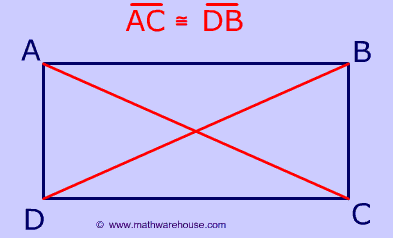
Indeed, clarity about these ideas is one of the many reasons for teaching this material at school. The complementary ideas of a ‘property’ of a figure, and a ‘test’ for a figure, become particularly important in this module. Considerable guidance in such ideas is normally required in Year 8, which is consolidated by further discussion in later years. Because of its systematic development, it provides an excellent introduction to proof, converse statements, and sequences of theorems. The material in this module is suitable for Year 8 as further applications of congruence and constructions. Some ruler-and-compasses constructions of them are developed as simple applications of the definitions and tests.Is a parallelogram or rectangle − again, congruence is mostly required. Tests for them are established that can be used to check that a given quadrilateral.Their significant properties are proven, mostly using congruence.The parallelogram and rectangle are carefully defined.Each congruence proof uses the diagonals to divide the quadrilateral into triangles, after which we can apply the methods of congruent triangles developed in the module, Congruence.

This module will deal with two of them − parallelograms and rectangles − leaving rhombuses, kites, squares, trapezia and cyclic quadrilaterals to the module, Rhombuses, Kites, and Trapezia.Īpart from cyclic quadrilaterals, these special quadrilaterals and their properties have been introduced informally over several years, but without congruence, a rigorous discussion of them was not possible. In contrast, there are many categories of special quadrilaterals. There are only three important categories of special triangles − isosceles triangles, equilateral triangles and right-angled triangles.


 0 kommentar(er)
0 kommentar(er)
